You are given a rows x cols matrix grid representing a field of cherries where grid[i][j] represents the number of cherries that you can collect from the (i, j) cell.

You have two robots that can collect cherries for you:

• Robot #1 is located at the top-left corner (0, 0), and
• Robot #2 is located at the top-right corner (0, cols - 1).

Return the maximum number of cherries collection using both robots by following the rules below:

• From a cell (i, j), robots can move to cell (i + 1, j - 1), (i + 1, j), or (i + 1, j + 1).
• When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
• When both robots stay in the same cell, only one takes the cherries.
• Both robots cannot move outside of the grid at any moment.
• Both robots should reach the bottom row in grid.

Example 1:

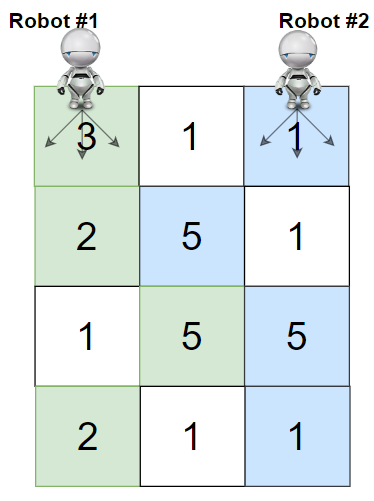
Input: grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]]
Output: 24
Explanation: Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.

Example 2:

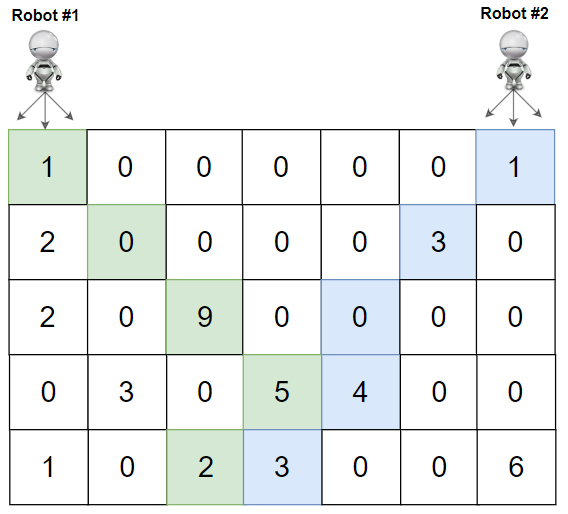
Input: grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]
Output: 28
Explanation: Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.

Constraints:

• rows == grid.length
• cols == grid[i].length
• 2 <= rows, cols <= 70
• 0 <= grid[i][j] <= 100

这道题目长着动态规划的脸。子问题看起来很明显：针对 Grid 中的每一格，其上一层都只有三种情况。如果只有一个机器人，这就是一道非常基础的动态规划题，最多给个中等难度。但是这里有两个机器人，因此思路也陷入僵局。

好在问题的 Solution 写得非常清楚，我们需要同时移动两个机器人。我之前的思路过于局限。之前我认为 DP 是一种填格子游戏，把格子填满就是胜利。这一题告诉我它可以往自己划定的格子里填数，而不是限死在题设的格子里。

我们定义 dp 为 number[][][] 。这个三位数组中的第二维是 robot1 的位置，第三维是 robot2 的位置。由于有两个机器人，前一列共有 3*3 = 9中情况。我在最初的解法里把9中情况都列了出来，随后优化成了两个循环。据此写出的解法为：

/**
 * @param {number[][]} grid
 * @return {number}
 */
var cherryPickup = function(grid) {
    let dpCache = []
    for(let i=0; i<grid.length; i++) {
        dpCache.push([])
        for (let j=0; j<grid[0].length; j++) {
            dpCache[i][j] = []
        }
    }

    let max = 0
    
    function dp(r, i, j) {
        if (i < 0 || i >= grid[0].length || j<0 || j>=grid[0].length) return -Infinity
        if (r===0) {
            const rst = i === 0 && j === grid[0].length-1
                ? grid[r][i] + grid[r][j]
                : -Infinity
            dpCache[r][i][j] = rst
            return rst
        }
        if (dpCache[r][i][j]) return dpCache[r][i][j]
        
        let rMax = -Infinity
        
        for(let ii = i-1; ii<=i+1; ii++) {
            for (let jj = j-1; jj<=j+1; jj++) {
                rMax = Math.max(rMax, dp(r-1, ii, jj))
            }
        }

        const rst = i === j ? rMax + grid[r][i] : rMax + grid[r][i] + grid[r][j]
        dpCache[r][i][j] = rst
        if (rst > max) max = rst
        return rst
    }
    
    for(let i=0; i < grid[0].length; i++) {
        for (let j=0; j<grid[0].length; j++) {
            dp(grid.length-1, i, j)
        }
    }
        
    return max
};

这是一个不太好的解法。可以看到我们在最后 dp 了 row ^ 2 次，因为 robot1 和 robot2 最后可能会在任何位置。更大的问题是：不是每一个初始位置都能到达这些重点的，但是我们的初始位置是确定的。

如果我把 row[0] 中的每一个元素设置为对应的 robot1 + bobot2 的和，那么我们就得到一个更通用的解：机器人可以在任何初始位置。但是对这一题，我不得不吧其它位置设置成 -Infinity ，然后这些额外的解就变得非常累赘。我们应该从上向下遍历。

/**
 * @param {number[][]} grid
 * @return {number}
 */
var cherryPickup = function(grid) {
    let dpCache = []
    for(let i=0; i<grid.length; i++) {
        dpCache.push([])
        for (let j=0; j<grid[0].length; j++) {
            dpCache[i][j] = []
        }
    }
    
    function dp(r, i, j) {
        if (i < 0 || i >= grid[0].length || j<0 || j>=grid[0].length) return -Infinity
        if (dpCache[r][i][j]) return dpCache[r][i][j]
        
        let rMax = 0
        // 注意这个if判断，很重要
        if (r < grid.length - 1) {
            for(let ii = i-1; ii<=i+1; ii++) {
                for (let jj = j-1; jj<=j+1; jj++) {
                    rMax = Math.max(rMax, dp(r+1, ii, jj))
                }
            }
        }
        
        let rst = (i === j ? grid[r][i] : grid[r][i] + grid[r][j]) + rMax

        dpCache[r][i][j] = rst
        return rst
    }
    
    return dp(0, 0, grid[0].length-1)
};

这并不容易。思路上我们先拿到当前格的值，然后再加上9种可能的情况中最大的那个值。当我们遍历到最后一列的时候，我们不应该再继续dp，而是直接返回当前格的值就可以。这时候第一列的格子里装的是走到最后一列时最大值时多少，而且只有 dpCache[0][grid[0].length-1]有值。这正是我们想要的效果。要知道，当我们自下而上进行DP的时候可是每一个格子都填满了。

这种做法对我而言也是冲击性的。这是我第一次从上到下进行DP，所以写下这篇博客作为记录。