Minimum Height Trees

A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.

Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [ai, bi] indicates that there is an undirected edge between the two nodes ai and bi in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h)) are called minimum height trees (MHTs).

Return a list of all MHTs' root labels. You can return the answer in any order.

The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.

Example 1:

Input: n = 4, edges = [[1,0],[1,2],[1,3]]
Output: [1]
Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.

Example2:

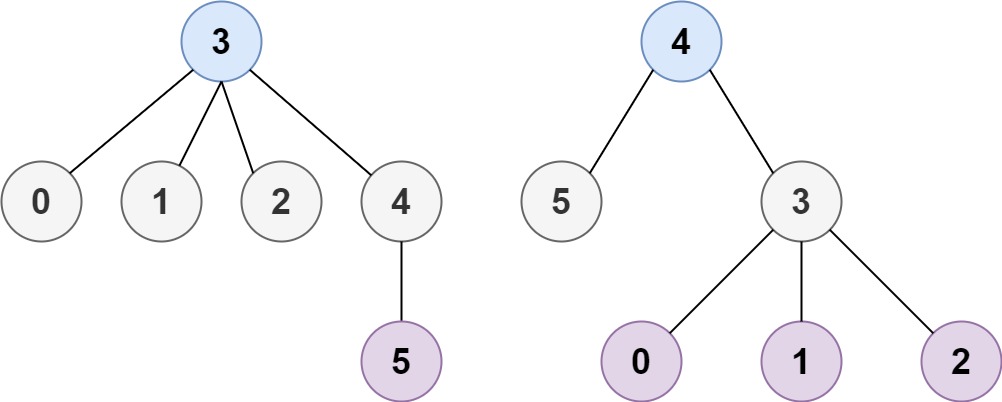
Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
Output: [3,4]

Constraints:

• 1 <= n <= 2 * 104
• edges.length == n - 1
• 0 <= ai, bi < n
• ai != bi
• All the pairs (ai, bi) are distinct.
• The given input is guaranteed to be a tree and there will be no repeated edges.

这是一道 BFS 算法题。当我们拿到一个图，并且看到最小高度这样的词语的时候，这便是我们的第一印象。这道题目给的入参有点恶心，我们必须自己实现一个邻接表。

但是，按照常规的 BFS 思路，我们会陷入僵局。不过至少我们可以把每个节点作为 root，然后记录最小的高度。这一解法显然不理想。

首先让我们回顾一下 BFS 和 DFS。这两个算法几乎完全一样，区别只是使用的数据结构。BFS 使用的是队列，DFS 使用的是栈。然后，我们随便抓一个节点进队列（或者栈），从该节点开始遍历。然后如果我们每一轮遍历需要做点事情，就很有可能要记录一下每一轮有多少节点，这便会要在 while 循环里塞一个 for 循环。

这里讨论一下 seen。 seen 是一个存放了已见节点的数组（或者其它你喜欢的数据结构）。你会发现我给出的代码里没有 seen，这是因为这一题只会把符合条件的节点推到 queue 里面去，不存在多次遍历问题。通常情况下是无法省略这一数据的。

而这一题的玄机也在于每一轮塞到队列的节点是什么。我们可以把只有一条边的节点塞进去，这样到最后只剩下一个或者两个的时候，就是问题的解。

/**
 * @param {number} n
 * @param {number[][]} edges
 * @return {number[]}
 */
var findMinHeightTrees = function(n, edges) {
    let adj = Object.fromEntries(Array(n).fill(undefined).map((j, i) => [i, []]))
    const queue = []
    let remain = n
    edges.forEach(([left, right]) => {
        adj[left].push(right)
        adj[right].push(left)
    })
    
    Object.keys(adj).forEach(v => (adj[v].length === 1) && queue.push(+v))
    
    while(remain > 2) {
        let size = queue.length
        for(let i=0; i<size; i++) {
            let crt = queue.shift()
            let neighbor = adj[crt][0]
            adj[neighbor].splice(
                adj[neighbor].indexOf(crt),
                1
            )
            delete adj[crt]
            remain--
            if (adj[neighbor].length === 1)
                queue.push(neighbor)
        }
    }
    
    return Object.keys(adj)
};

---

127. Word Ladder

A transformation sequence from word beginWord to word endWord using a dictionary wordList is a sequence of words beginWord -> s1 -> s2 -> ... -> sk such that:

• Every adjacent pair of words differs by a single letter.
• Every si for 1 <= i <= k is in wordList. Note that beginWord does not need to be in wordList.
• sk == endWord

Given two words, beginWord and endWord, and a dictionary wordList, return the number of words in the shortest transformation sequence from beginWord to endWord, or 0 if no such sequence exists.

Example 1:

Input: beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
Output: 5
Explanation: One shortest transformation sequence is "hit" -> "hot" -> "dot" -> "dog" -> cog", which is 5 words long.

Example 2:

Input: beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
Output: 0
Explanation: The endWord "cog" is not in wordList, therefore there is no valid transformation sequence.

Constraints:

• 1 <= beginWord.length <= 10
• endWord.length == beginWord.length
• 1 <= wordList.length <= 5000
• wordList[i].length == beginWord.length
• beginWord, endWord, and wordList[i] consist of lowercase English letters.
• beginWord != endWord
• All the words in wordList are unique.

这曾经是一道MEDIUM难度的题目，但是现在变成了HARD。我们再次看到了 『最少步骤』 这样的词语。一旦领悟这一题要用BFS，离做出题目就不远了。好在这题有些优化点，勉强算是够格吧。

需要注意的是，入参的wordlist需要转换成Set，不然会超时。

/**
 * @param {string} beginWord
 * @param {string} endWord
 * @param {string[]} wordList
 * @return {number}
 */
var ladderLength = function(beginWord, endWord, wordList) {
    const queue = [beginWord], visited = new Set(), list = new Set(wordList)
    let count = 1
    
    while(queue.length) {
        count++
        const size = queue.length
        
        for (let i=0; i<size; i++) {
            const crt = queue.shift()
            
            for (let j=0; j<crt.length; j++) {
                for (let k='a'; k<='z'; k=String.fromCharCode(k.charCodeAt(0)+1)) {
                    const newWord = crt.substr(0, j) + k + crt.substr(j+1)
                    if (list.has(newWord) && !visited.has(newWord)) {
                        if (newWord === endWord) return count
                        queue.push(newWord)
                        visited.add(newWord)
                    }
                }
            }
        }
    }

    return 0
};

---

847. Shortest Path Visiting All Nodes

You have an undirected, connected graph of n nodes labeled from 0 to n - 1. You are given an array graph where graph[i] is a list of all the nodes connected with node i by an edge.

Return the length of the shortest path that visits every node. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.

Example 1:

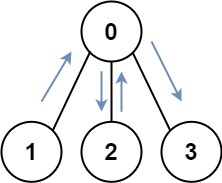
Input: graph = [[1,2,3],[0],[0],[0]]
Output: 4
Explanation: One possible path is [1,0,2,0,3]

Example 2:

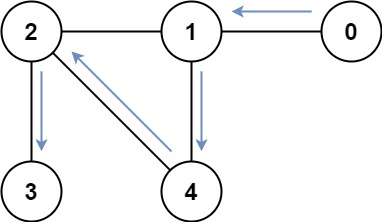
Input: graph = [[1],[0,2,4],[1,3,4],[2],[1,2]]
Output: 4
Explanation: One possible path is [0,1,4,2,3]

Constraints:

• n == graph.length
• 1 <= n <= 12
• 0 <= graph[i].length < n
• graph[i] does not contain i.
• If graph[a] contains b, then graph[b] contains a.
• The input graph is always connected.

个人很喜欢这倒题目。BFS相关的题目很多，当玩家觉得自己已经掌握BFS的时候，这一题可以提供新的着眼点。

上面我们讨论了 seen ，或者 visited ——不管你喜欢用什么变量名。visited 对BFS 很重要，它可以确保我们不会推入已经访问过的节点。如果不加入 visited 就会形成死循环。

这一题拓展了visited 的范围。visited不止可以储存节点而已。

下面我们结合题目来说。

我们应该用BFS吗？很有可能。题目中出现了最短这样的字眼，我们的DNA此时应该有反应了。

但是，我们又会发现这题好像不太好用BSF，因为它是可以往回走的。如果我们记录路径的话，visited就失去了意义，因为遍历的时候路径必然是不同的。并且，这样进行计算queue 的空间很快就会爆满。

如果我们依然顺着这条路走下去，会遇到更严重的麻烦：这个图是可能存在环的。作为一个无向图，它想来点环可太容易了。然后，这个环很不好处理。

visited的作用是，去除遍历过程中的重复状态。 那么这一题的重复状态是什么呢？

答案是，当你达到某个节点时，有几个节点被访问到了。

一旦我发现，到下一个节点时，没有新增访问过的节点，就代表这条路可以舍弃了。因为已经有更的路径达到相同的结果了。我们可以用二进制表示节点是否被访问，0代表没有，1代表访问过了。这里用数组也可以，用二进制是因为方便比较。

比如说，对于例1，我们先这样走 0 -> 2 -> 0，这时候我们有三个相邻点。假设我们选择1，即0 -> 2 -> 0 -> 1，状态为1-7(7即0111，代表0，1，2都访问过了)，该状态没有出现过，可以推入队列中。

现在我们再选择2，状态为 2-5(5 即 0101，代表0和2都访问过了)，这个状态显然是重复的，就不必推入queue中了。

由此，我们使用{节点}-访问过的节点的二进制表示来代表状态。一旦想清楚这一点，接下来就是个细节比较多的BFS了。

/**
 * @param {number[][]} graph
 * @return {number}
 */
var shortestPathLength = function(graph) {
    let count = 0
    const queue = []
    const visited = new Set()
    
    for(let i=0; i<graph.length; i++) {
        if (graph[i].length)
            queue.push(i + '-' + (1 << i))
    }
    
    if (queue.length === 0) return 0

    while(queue.length) {
        count++
        const size = queue.length
        for (let i=0; i<size; i++) {
            const crt = queue.shift()
            const [node, status] = crt.split('-')

            for (let j=0; j<graph[node].length; j++) {
                const newStatus = status | 1 << graph[node][j]
                if (newStatus === (1<<graph.length)-1) {
                    return count                        
                }
                const newRecord = graph[node][j] + '-' + newStatus
                if (!visited.has(newRecord)) {
                    visited.add(newRecord)
                    queue.push(newRecord)
                }
            }
        }
    }
};

这一题queue的初始状态也很有趣。一般来说，我们会在queue上放上任意初始节点，但是这题从不同的节点开始会得出不同的最小值。所以我最初的解法每个顶点都遍历了一遍。这样可以通过，但是很慢。

随后看了其他人的解法，发现可以一开始就把每个节点的初始状态都放上去，于是时间大幅度缩短。

最后感谢 郭郭wg 的解题视频【升维 BFS 巧妙应用】leetcode 847. Shortest Path Visiting All Nodes。我总是从郭郭老师那里找答案，就在这里统一感谢下。